알고리즘 이론 2강. 점근적 표기법(Asymptotic notation)

 

[점근적 표기(Asymptotic notation)]

: 알고리즘의 수행 시간을 표기하기 위해, 필수적인 부분에 집중하고 불필요한 상세들을 무시해야 한다.

예시) f(n) = n^2+n+100 일때 가장 차수가 높은 n^2에 집중 => 시간 복잡도 : O(n^2)

: 아무리 높은 수가 낮은 차수에 붙어도, n이 무한대로 가는 길에선 제일 높은 차수의 증가폭이 넘사벽.

 

# 점근적 표기법 종류

• O-표기 : 상한 표기법
• Θ-표기
• Ω-표기 : 하한 표기법

 

 

 

[O-표기법] (= Big-O)

: 점근적 상한만 알고 있을때 사용하는 표기법 (= 최악의 경우에도 이 기준 넘지 않는다)

# 정의

: 주어진 함수 g(n)에 대해 빅오(O(g(n))을 다음과 같은 함수의 집합으로 나타낸다.

상한 표기법 정의

예시1) 7n-2 이 O(n)임을 증명해라. sol)  c>0이고 no>=1 일때(전제조건) n >= no에 대해 7n-2 <= cn인 c,no이 존재하는가? => c = 7, no = 1 일때 true(존재)   예시2) 3n^3+20n^2+5 이 O(n^3)임을 증명해라. sol)  c>0이고 no>=1 일때(전제조건) 생략 => c=4, no = 21 존재 => true

 

 

 

[Ω-표기법](Omega)

: 점근적 하한만 알고 있을때 사용하는 표기법(=아무리 빨라도 이 기준보다 빠를수 없다)

# 정의

하한 표기법 정의( O가 아니라 Ω임)

 

 

 

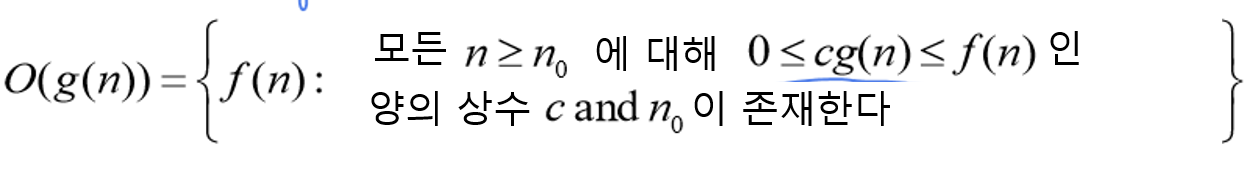
[Θ-표기법](Theta)

: 상한과 하한을 둘다 알고 있을때 표기법(상한 표기법, 하한 표기법 포함관계)

 

# 정의

상하한 표기법 정의

 

 

 

[표기법간의 포함관계]

: Θ-표기법이 가장 강력한 표기 방법이다.

 => f(n) = Θ(g(n) 이면 f(n) = O(g(n)), f(n) = Ω(g(n))이고, 역도 성립한다.

 

 

 

[표기법 증명 방법(숙지!!)]

우선 바운드 관련 증명을 하라 할때 f(n)이 표기법(g(n))임을 증명하라는 문제로 출제된다.

이때, c*g(n) ><= f(n) 형태로 만든뒤, c ><= f(n) / g(n) 형태로 바꿔준다.

여기서, n부분에 1부터 넣어주며 c를 구하고, 이 값이 성립하는 no과 c값인지 하나씩 확인해주면된다.

 

* 세타 표기법 증명은 상한 증명, 하한 증명으로 둘다 증명하면 자연스럽게 증명됨.

 

 

 

[바운드 증명 예시]

1. 5n^2 – 15n + 100이 Θ(n^2)임을 보여라.

풀이) 1단계. 우선 O(n^2)임을 증명(상한 존재함을 증명) 모든 n>no에 대해 5n^2-15n+100 <= cn^2이 성립하는 양의 상수 c와 no을 구한다. c >= 5-15/n + 100/n^2 c = 90, no = 1일때 성립 => 존재. 2단계. Ω(n^2)임을 증명(하한 존재함을 증명) 모든 n>no에 대해 5n^2-15n+100 >= cn^2이 성립하는 양의 상수 c와 no을 구한다. c <= 5- 15/n + 100/n^2 c = 1.25, no = 4일때 성립 => 존재. 3단계. 상한과 하한이 모두 n^2임을 증명했으니 Θ(n^2)임을 자연스럽게 증명 가능.

2. 5n^2이 O(n)인가?

c*n >= 5n^2이 성립되는 c와 no값 있는지 확인. => c >= 5n : 성립 불가능!!! (n0이 특정 값이여도 n이 증가하는 이상 만족되는 c없음)

 

 

 

[일반적인 규칙]

: 위와 같이 예시를 보면 알수 있는게 하나 있는데, 바로 낮은 차수의 값들이 생략될수 있다는 것을 있다.

• 곱하기 형태의 상수 생략 가능 : 14n^2 => n^2
• 낮은 차수 생략 가능
• a > b일때 n^a가 n^b 점령
• a > b일때 a^n이 b^n 점령
• 지수함수가 다항식(n승) 점령
• 다항식이 로그함수 점령
• 변수가 다르면 생략 X : n^2 + m등

 

 

 

[일반적인 표기 기준]

- O(1)

  : 상수. 입력값의 크기와 무관

  : 사칙연산, if문, 일정범위(상수값)계산, 링크드리스트에서 삭제(time과 관련있음)

 

- O(logn)

  : 반복문, 입력값의 일부분을 버림(half)

  : 이진 검색 등

 

- O(n)

  : 선형. 입력 값에 각 요소들에 대한 작업.

  : 링크드리스트에서 검색, 배열내 최대값 원소.

 

- O(nlogn)

  : 비선형. 분할과 정복 알고리즘.

  : 병합 정렬 등

 

- O(n^2)

  : 2중 반복문

  : 삽입정렬, 선택정렬 등

 

- O(2^n)

  : 지수승. 모든 부분 집합 검색, 브루노 포스(모든 경우 검색)

 

- O(n!)

  : 모든 순열(permutations) 검색